| Главная Онлайн-расчеты Научный калькулятор | |
|
Перпендикулярность плоскостей
Определение. Две плоскости называются перпендикулярными,
если линейный угол при ребре двугранного угла между этими плоскостями — прямой.
Признак перпендикулярности плоскостей. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны. 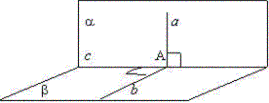 Доказательство. Пусть a и ? - две пересекающиеся плоскости, с — прямая
их пересечения и а — прямая перпендикулярная
плоскости ? и лежащая в
плоскости a. А — точка пересечения прямых
a
и с. В плоскости ? из точки А восстановим перпендикуляр,
и пусть это будет прямая b. Прямая а перпендикулярна плоскости ?,
а значит она перпендикулярна и любой прямой в этой плоскости, то есть прямые b и
с перпендикулярны. Угол между прямыми а и Ь — линейный угол при ребре двугранного угла между плоскостями a
и ? и равен он 90°, так как прямая
а перпендикулярна прямой b (по доказанному). По
определению плоскости a и ? перпендикулярны.
Доказательство. Пусть a и ? - две пересекающиеся плоскости, с — прямая
их пересечения и а — прямая перпендикулярная
плоскости ? и лежащая в
плоскости a. А — точка пересечения прямых
a
и с. В плоскости ? из точки А восстановим перпендикуляр,
и пусть это будет прямая b. Прямая а перпендикулярна плоскости ?,
а значит она перпендикулярна и любой прямой в этой плоскости, то есть прямые b и
с перпендикулярны. Угол между прямыми а и Ь — линейный угол при ребре двугранного угла между плоскостями a
и ? и равен он 90°, так как прямая
а перпендикулярна прямой b (по доказанному). По
определению плоскости a и ? перпендикулярны.
Теорема 1. Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то это перпендикуляр полностью лежит в первой плоскости. 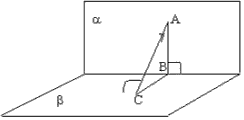 Доказательство. Пусть a и ? -
перпендикулярные плоскости и с — прямая их пересечения, А — точка
лежащая в плоскости
a и не принадлежащая прямой с. Пусть перпендикуляр к плоскости ? проведенный из точки А, не лежит в плоскости a, тогда точка С – основание этого перпендикуляра лежит в плоскости ? и
не принадлежит прямой с. Из точки А опустим перпендикуляр АВ
напрямую с. Прямая АВ перпендикулярна плоскости (использую теорему 2). Через прямую АВ и точку С проведем плоскость ?
(прямая и точка определяют плоскость, причем только одну). Мы видим, что в плоскости ? из одной точки А на прямую ВС проведено два перпендикуляра, чего быть не
может, значит прямая АС совпадает с прямой АВ, а прямая АВ в
свою очередь полностью лежит в плоскости a.
Доказательство. Пусть a и ? -
перпендикулярные плоскости и с — прямая их пересечения, А — точка
лежащая в плоскости
a и не принадлежащая прямой с. Пусть перпендикуляр к плоскости ? проведенный из точки А, не лежит в плоскости a, тогда точка С – основание этого перпендикуляра лежит в плоскости ? и
не принадлежит прямой с. Из точки А опустим перпендикуляр АВ
напрямую с. Прямая АВ перпендикулярна плоскости (использую теорему 2). Через прямую АВ и точку С проведем плоскость ?
(прямая и точка определяют плоскость, причем только одну). Мы видим, что в плоскости ? из одной точки А на прямую ВС проведено два перпендикуляра, чего быть не
может, значит прямая АС совпадает с прямой АВ, а прямая АВ в
свою очередь полностью лежит в плоскости a.
Теорема 2. Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости. 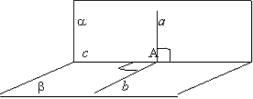 Доказательство. Пусть a и ? - две
перпендикулярные плоскости, с — прямая их пересечения и а — прямая
перпендикулярная прямой с и лежащая в
плоскости a. А — точка пересечения прямых а и с. В
плоскости ? из точки А восстановим перпендикуляр,
и пусть это будет прямая b. Угол
между прямыми а и b — линейный
угол при ребре двугранного угла между плоскостями a и ? и равен он 90°, так как плоскости a
и ? перпендикулярны. Прямая а перпендикулярна
прямой b (по доказанному) и прямой с по условию. Значит
прямая а перпендикулярна плоскости ? (по признаку перпендикулярности прямой и плоскости).
Доказательство. Пусть a и ? - две
перпендикулярные плоскости, с — прямая их пересечения и а — прямая
перпендикулярная прямой с и лежащая в
плоскости a. А — точка пересечения прямых а и с. В
плоскости ? из точки А восстановим перпендикуляр,
и пусть это будет прямая b. Угол
между прямыми а и b — линейный
угол при ребре двугранного угла между плоскостями a и ? и равен он 90°, так как плоскости a
и ? перпендикулярны. Прямая а перпендикулярна
прямой b (по доказанному) и прямой с по условию. Значит
прямая а перпендикулярна плоскости ? (по признаку перпендикулярности прямой и плоскости).
|
|