Теорема 7. Объем пирамиды равен одной трети произведения площади основания на высоту.
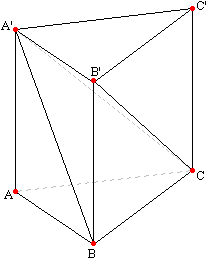Докажем на примере треугольной пирамиды. Будем исходить из треугольной призмы. Проведем плоскость через вершину A' верхнего основания призмы и противолежащее ребро ВС нижнего основания. Эта плоскость отсечет от призмы треугольную пирамиду A'АВС. Оставшуюся часть призмы разложим на жва тела, проведя плоскость через диагонали A'С и B'C боковых граней. Полученные два тела также являются пирамидами. Считая треугольник A'B'C' основанием одной из них, а С её вершиной, увидим, что её основание и высота такие же, как и у первой отсеченной нами пирамиды, поэтому пирамиды A'АВС и CA'B'C' равновелики. Кроме того, обе новые пирамиды CA'B'C' и A'B'ВС также равновелики - это станет ясным, если примем за их основания треугольники ВСB' и B'CC'. Пирамиды CA'B'C' и A'B'ВС имеют общую вершину A', а их основания расположены в одной плоскости и равны, следовательно, пирамиды равновелики. Итак, призма разложена на три равновеликие между собой пирамиды; объем каждой из них равен одной трети объема призмы. Так как форма основания несущественна, то, вообще, объем n-угольной пирамиды равен одной трети объема призмы с тое же высотой и тем же (или равновеликим) основанием. Вспоминая формулу, выражающую объем призмы, V=Sh, получим окончательный результат: Площадь боковой поверхности произвольной пирамиды равна сумме площадей её боковых граней. Специальную формулу для выражения этой площади имеет смысл дать в случае:
Теорема 8. Если все апофемы пирамиды равны, то площадь её боковой поверхности можно вычислить по формуле: Из этой теоремы можно получить подобные:
Теорема 8.1. Если все боковые грани пирамиды наклонены к плоскости основания под одинаковым углом, то площадь её боковой поверхности можно вычислить по формуле: Теорема 8.2. Если пирамида правильная, то площадь её боковой поверхности можно вычислить по формуле: При нахождении площади поверхности пирамиды, необладающей ни одним из перечисленных признаков, осуществляется вычисление площадей отдельных граней, а затем производится их суммирование.