Задача №199

Дан куб АВСDА₁В₁С₁D₁,Найдите угол между прямыми АD₁ и ВМ, где М - середина ребра DD₁.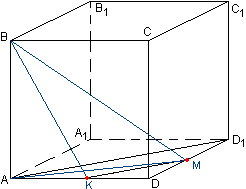
Для удобства решения развернем куб так, как показано на рисунке. Вспомним определение: Углом между скрещивающимися прямыми называется угол между двумя прямыми, параллельными им и проходящими через произвольную точку. Пусть точка М будет произвольной точкой, тем более, что одна из скрещивающихся прямых ВМ уже через неё проходит. Нам остается сделать параллельный переход для AD₁. Для этого через точку М в плоскости ADD₁A₁ проведем прямую МК параллельно AD₁. Угол ВМК - искомый.
Вспомним формулу двойного проектирования. Пусть ВМ - наклонная, МК - прямая в плоскости. Тогда АМ - проекция. Запишем формулу:
cos∠ВМК=cos∠BMA * cos∠AMK
Обозначим ребро куба за а. Из прямоугольного треугольника АМD:

Из прямоугольного треугольника АВМ: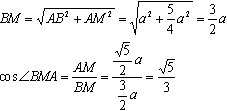

Из теоремы о том, что параллельные прямые отсекают на сторонах угла пропорциональные отрезки, заключаем, что точка К - середина AD. Из прямоугольного равнобедренного треугольника KDM:

Найдем косинус угла АМК через разность углов АМD и KMD:
cos∠AMK=cos(∠AMD-∠KMD)=cos∠AMD * cos∠KMD+sin∠AMD * sin∠KMD

Осталось подставить найденные значения в формулу: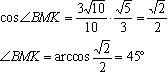

Есть еще один способ:
Из прямоугольного треугольника АВК найдем ВК:
Теперь в треугольнике МКВ запишем теорему косинусов: