Задача №24

Основание пирамиды MABCDEF — правильный шестиугольник ABCDEF со стороной 8 см. Ребро AM перпендикулярно основанию и равно 8 см. Найдите двугранный угол между гранью МED и плоскостью основания.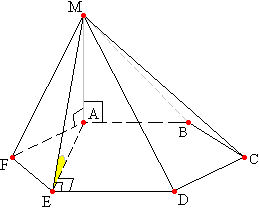

Определим двугранный угол между этими плоскостями. Для этого из точки А опустим перпендикуляр на ребро ED. Этот перпендикуляр упадет в точку Е (Почему?). По теореме о трех перпендикулярах боковое ребро МЕ перпендикулярно ребру основания ED. А угол МЕА является линейным углом двугранного угла меджу основанием и боковой гранью MED.

Потому что...
Рассмотрим основани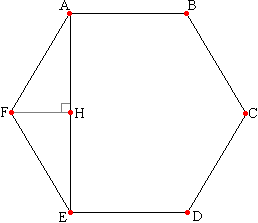е:
Известно, что каждый угол правильного шестиугольника равен 120°. Рассмотрим треугольник AEF – он равнобедренный по определению (FA=FE). Проведем высоту FH. По свойству высоты равнобедренного треугольника, проведенной из вершины, она является также биссектрисой и медианой. Т.е. ∠EFH=∠AFH=1/2∠AFE=60° и АН=1/2АЕ.
Далее из прямоугольного треугольника EFH, зная, что сумма острых углов ранва 90°, получаем: ∠FEH=90° - ∠EFH = 30°.
Теперь - ∠AED=∠FED - ∠FEH = 120° - 30° = 90°. Поэтому прямая АЕ перпендикулярна ED.
Из треугольника АFH найдем АН: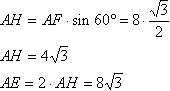

Прямая МА перпендикулярна основанию, значит, она перпендикулярна любой прямой плоскости основания, в том числе и прямой АЕ. Т.е. треугольник МАЕ прямоугольный. В нем нам известны два катета, и мы можем вычислить тангенс искомого угла: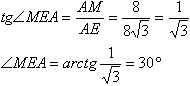